Nous vous proposons ici une présentation générale de la classe puzzle, ainsi que des activités créées et testées par le groupe.
Recherche et formation – Enseignement des mathématiques et de l'informatique

Nous vous proposons ici une présentation générale de la classe puzzle, ainsi que des activités créées et testées par le groupe.
Cette démarche d’investigation a été proposée dans des classes à tous les niveaux du collège.
Les élèves doivent mobiliser leurs connaissances sur le périmètre d’un cercle et l’utilisation d’une échelle pour déterminer la distance entre deux athlètes au départ du 400 m.
Les élèves vont être amenés à :
Modéliser : (Transmaths)
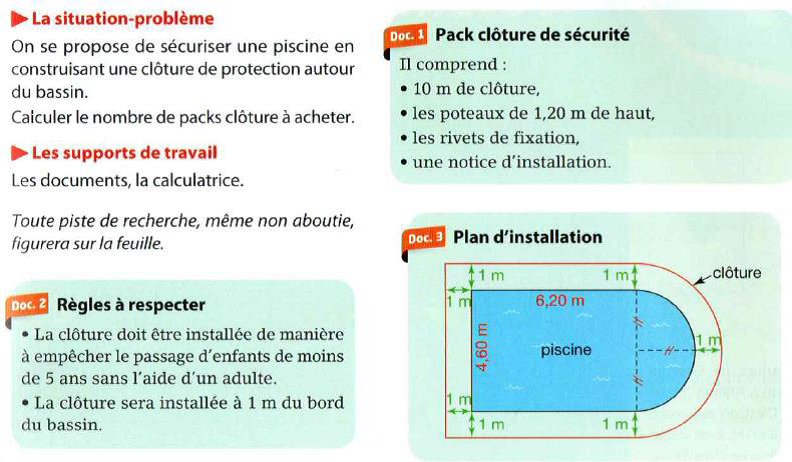
Les élèves doivent calculer le périmètre d’une figure complexe
Echelle : On peut proposer aux élèves des problèmes avec une échelle. On peut penser aux problèmes googlemath de Jean-Yves Labouche sur le site « mon classeur de maths ». Des problèmes comme « Des fleurs pour la reine » ou « une pêche royale » nécessitent des mesures et des calculs sur les aires.
Pour chacun des groupes :
Equivalent de deux séances à répartir sur trois créneaux :
Les élèves sont organisés en groupes ou en individuel – Nous réalisons le travail suivant en plénière.
Vue aérienne d’un stade : « Dans ce stade, des épreuves d’athlétisme ont lieu. Où se font le départ et l’arrivée pour le 100 m? Pour le 400 m ? »
Les élèves interagissent en groupes, nous leur disons qu’ils peuvent faire des marques au crayon de bois sur la vue aérienne distribuée. Nous circulons, certains groupes indiquent qu’ils ne savent pas, d’autres donnent les bons départs et/ou arrivées.
En plénière : « Nous allons visionner deux vidéos des JO de Tokyo en 2021. Nous commençons par la finale du 100 m dames. ». Lien : https://ladigitale.dev/digiview/#/v/66ff9b09273e9
Questionnement : Que remarquez-vous ?
Attendu avant de passer à la suite : « Ils partent en dehors de la piste principale »
Information à donner : La ligne droite de la piste principale fait donc moins de 100 mètres, elle fait en réalité environ 89 mètres.
En plénière : « Nous allons visionner la deuxième vidéo qui est la finale du 400 m dames. ». Lien : https://ladigitale.dev/digiview/#/v/66ff9e6990e5b
Que remarquez-vous ?
Réactions des élèves : celui à l’extérieur est avantagé, il a moins de distance à parcourir.
Relance si besoin : « L’athlète qui part au couloir 7 a donc été avantagée, elle est partie devant, c’est normal qu’elle ait gagné la course. La course n’est pas équitable. »
Attendu avant de passer à la suite :
En plénière : Quelle question mathématique peut-on se poser ?
Relance : Vous êtes les organisateurs de la course, qu’est-ce que vous devez savoir ?
Lors du départ du 400 mètres, les coureurs ne sont pas tous placés sur la même ligne.
Quelle distance sépare les athlètes pour que la course soit équitable ?
Certains élèves supposent à juste titre que la distance est identique entre deux coureurs. On peut les interroger sur la validité de leur conjecture plus tard.
Pour calculer la longueur du tour de piste dans le couloir n°1 : L x 2 + π x d où d est le diamètre du demi-cercle passant par le couloir n°1.
Pour calculer la longueur du tour de piste dans un autre couloir : L x 2 + π x d’ où d’ est le diamètre du demi-cercle passant par cet autre couloir.
Ordre de grandeur sur la réponse attendue : Chaque départ est décalé de 7 m environ.
Le temps de correction et de bilan est primordial. Les élèves ont travaillé pendant un temps long et un retour sur leurs stratégies, leur rédaction sur la fiche de narration. La DI propose également un travail un peu différent du travail classique en classe : un bilan sur les mathématiques utilisées et sur la démarche scientifique est intéressant à mener.
Nous utilisons des productions d’élèves pour des éléments de correction.
Les réunions en présentiel se tiendront pour cette année en salle L220 du bâtiment de Mathématiques de la Faculté des Sciences d’Angers.
Pour l’année 2024-2025, l’organisation a été modifiée pour répondre aux exigences de l’EAFC.
Les actions du groupe :
Cette démarche d’investigation a été proposée à des élèves de 6ème et de 5ème.
L’objectif est de permettre aux élèves de découvrir ou de retrouver les formules d’aire de figures usuelles.
Pour débuter ce problème, les élèves n’ont à disposition que la formule de l’aire d’un rectangle. Ils doivent, à la manière d’un mathématicien, écrire les formules d’aire de figures usuelles (triangle rectangle, parallélogramme, trapèze, triangle quelconque, losange)
Les élèves vont être amenés à :
Les productions ci-dessous sont issues d’un travail avec une classe de 5ème.
La correction permet de montrer les différentes procédures pour les calculs d’aires d’un losange et d’un parallélogramme. On observe que les différents découpages et assemblages se ramènent toujours à un rectangle.
Le bilan permet d’expliciter les « vraies » formules qui vont être utilisées dans les exercices, en particulier pour le triangle quelconque et le trapèze. Les élèves doivent observer que les formules d’aire des figures usuelles peuvent se retrouver à partir de la seule connaissance de l’aire d’un rectangle.
Cette activité a été testée au lycée général en classe de 2nde . Elle peut être réalisable en fin de cycle 4 ou en 1ère spécialité et technologique.
On propose aux élèves de réaliser une brique avec une feuille A4 en observant le patron de briques alimentaires et de calculer son volume. L’objectif est de modéliser par une fonction le volume de la brique afin d’en déterminer le maximum.
Dans cette activité, les élèves vont être amenés à :
Munir les groupes de 2 briques en carton de formats différents (soupe, crème anglaise, brique de lait, briquette de jus de fruits, …). Au préalable, il faut les découper, enlever les marges de soudure et les nettoyer avant de les scotcher pour obtenir la boîte de départ. Les soudures ajoutent une difficulté inutile pour le travail des élèves.

| Attention : En imaginant le patron d’une brique en mode portrait de la feuille A4 (briques allongées). Si on note x la largeur en cm, 29,7 – x est la hauteur et 21 ÷ 2 – x est la longueur. La fonction du volume définie par : f(x) = x (29,7 – x)(21÷ 2 – x), atteint environ son maximum pour x = 4,7 cm, soit 681,5 cm3 Cette fonction ne permet pas d’obtenir le volume maximal d’une brique répondant à la consigne. |
Les productions ci-dessous comportent des valeurs numériques intégrant les soudures de 0,5 cm.
En construisant nos briques, nous avons observé que les volumes n’étaient pas les mêmes. Nous cherchons à déterminer les dimensions de la boîte ayant le plus grand volume. Pour cela, nous avons utilisé le calcul littéral pour exprimer les dimensions de la boîte. En nommant x la largeur de la boîte, nous avons exprimé la longueur, la hauteur et le volume en fonction de x. A l’aide de la calculatrice ou du tableur, nous avons déterminé que le volume maximal est d’environ 797,98 cm3 pour x = 5,7168.
Cette démarche d’investigation a été proposée à des élèves de 5ème, 4ème, 3ème et de 2nde.
L’objectif est que les élèves mobilisent leurs connaissances arithmétiques en particulier celle sur la division euclidienne.
Dans cette activité, un raisonnement par disjonction de cas est proposé aux élèves.
Les élèves vont être amenés à :
Afin que les outils mathématiques soient disponibles chez les élèves, un travail autour de la division euclidienne est indispensable. On peut également envisager de travailler sur les raisonnements par disjonction de cas. Un prolongement de cette DI est possible avec l’algorithmique qui devra être préparé en amont, en particulier si les élèves utilisent le logiciel Scratch au collège.
Les élèves résolvent le problème en organisant leur démarche à l’aide de la fiche de narration de recherche.
A partir d’exemples, les élèves commencent par effectuer la D.E (division euclidienne) du nombre par 5. On obtient un quotient égal à q et les restes possibles sont : 0, 1, 2, 3 ou 4.
Quand les élèves ont des difficultés à trouver une méthode de résolution, on peut les encourager à travailler sur le chiffre des unités du montant à payer, en leur proposant de réfléchir à 10 nombres consécutifs (on n’évoquera pas directement « le chiffre des unités ») : « Que se passe-t-il entre 10 et 19 ? ». Si les élèves éprouvent des difficultés à trouver le nombre de pièces, on leur propose certains nombres : « Avec 11, combien faut-il de pièces ? ». Quand les élèves obtiennent le résultat correct, on les engage à poursuivre sur d’autres nombres consécutifs. Pour généraliser leur méthode de calcul à tous les autres nombres entiers, les élèves pourront dire qu’à chaque dizaine supérieure, il suffit d’ajouter 2 billets de 5 Soudoks.
De nombreux élèves pourront choisir cette démarche sur le chiffre des unités plutôt que celle sur les restes de la DE par 5. C’est une démarche, étant plus simple à formaliser, est à encourager auprès des élèves afin qu’ils trouvent les solutions du problème. Ensuite, nous pourrons les faire observer que certaines des solutions sont identiques.
Démarche possible sur le chiffre des unités :
La formalisation mathématique de cette méthode est plus compliquée et les pré-requis peuvent être limités à la disjonction de cas. Le raisonnement sur les restes de la DE n’est pas travaillé ici.
Pour mener cette correction et ces bilans en classe, nous pouvons projeter les productions des élèves. Voici un exemple :
Une correction possible pour la deuxième démarche possible

Le bilan mathématique pourra se concentrer sur la recherche de multiples de 5 pour trouver le nombre de billets.
On peut envisager de modifier l’énoncé en proposant des pièces de 3 Soudoks et des billets de 7 Soudoks. Cela permet d’éviter l’écueil du critère de divisibilité par 5 qui ne met pas en relief la résolution avec une division euclidienne par 5.
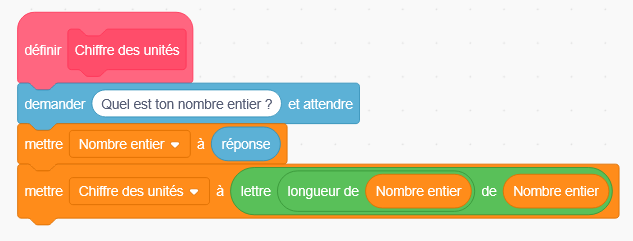
Le prolongement peut également se baser sur la deuxième démarche possible (sur le chiffre des unités). On peut écrire un bloc « chiffre des unités » sur Scratch permettant de récupérer le chiffre des unités d’un nombre afin d’écrire un script complet.
Le groupe a animé un atelier lors de la journée académique de 2023 et au colloque de la CORFEM en juin 2023. La réflexion du groupe a été présentée lors de la journée échange de pratique organisée par les IPR en partenariat avec l’IREM et l’APMEP à La Roche sur Yon (diaporama).
Les mercredis de 14h30-17h30 à l’INSPE salle 56 :
20/09/23 ; 22/11/23 ; 07/02/24 ; 03/04/24 ; 19/05/24
Programme de travail :
Les situations expérimentées et les analyses sont sur un espace de partage du groupe, si vous souhaitez expérimenter à votre tour, n’hésitez pas à nous contacter : sylvie.grau@univ-nantes.fr.
Les réunions se tiendront pour cette année en salle L220 du bâtiment de Mathématiques de la Faculté des Sciences d’Angers.
Pour l’année 2023-2024,
Les actions du groupe :