Archives de l’auteur : Guillaume Francois

Repas festif à La Quincaillerie

81 rue Marechal Joffre, 44000, Nantes France

En cas de problème, joindre Guillaume FRANÇOIS au 06 81 32 42 83

Plan

INSPE Nantes

4 Chemin de Launay Violette
44300 Nantes
Nantes

Coordonnées GPS

Latitude : 47.250463575637355°

Longitude : -1.5591044884299663°

Accès en tram

Ligne 2 – Arrêt Bourgeonnière (8 minutes à pieds) ou Ligne 2 – Arrêt École Centrale Audencia (10 minutes à pieds)

Accès en bus

Ligne 26 – Arrêt Freshe Blanc

Accès en voiture

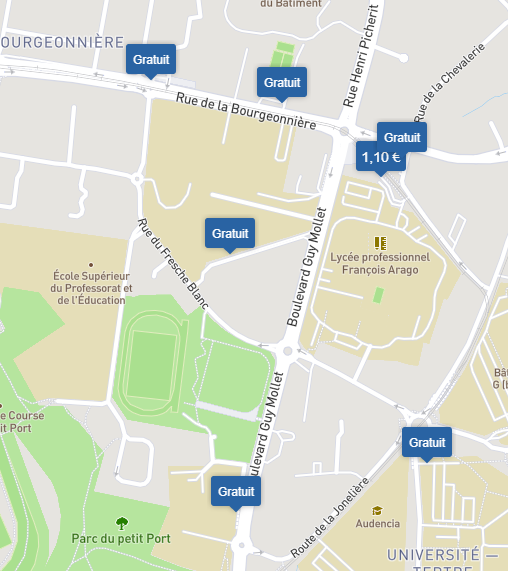
 ATTENTION pas de stationnement possible à proximité immédiate du site

Ci-dessous les parkings les plus proches :

Hébergement

Voici une liste d’hôtels dont l’emplacement et les tarifs nous ont parus intéressants.

Atelier 1 : Des croquis comme support de raisonnement – La CII Université

L’articulation entre différents registres (analytique, algébrique, géométrique) contribue à une meilleure appropriation des notions mathématiques. Les croquis réalisés à main levée jouent un rôle important dans cette articulation tant au lycée qu’à l’université.
Dans cet atelier nous vous proposons différents exemples mettant en évidence cette importance, notamment en ce qui concerne le raisonnement.

Atelier 2 : interférence entre langage usuel et logique – Christelle FITAMANT et Chloé SANCANDI de la CII Lycée.

Résumé à venir.

Atelier 3 : Implication : pierre angulaire du raisonnement – Denis GARDES et Dominique BERNARD de la CII Lycée.

On mènera une réflexion sur l’implication mathématique. Sa non compréhension est responsable de
difficultés majeures lors de raisonnements mathématiques.
On invitera les participants à se questionner autour de quelques problèmes, on définira ensuite la
notion d’implication, enfin on étudiera ses difficultés d’enseignement et d’apprentissage.

Atelier 4 : Des croquis comme support de raisonnement – Philippe LAC de la CII Lycée

On présentera , dans cet atelier, quelques  situations du niveau lycée pour lesquelles le lien entre la résolution mathématique et informatique sans aucune précaution peut conduire à des écueils. Il s’agira d’illustrer, par des exemples simples,  le fait que l’appel à l’outil informatique dans une résolution mathématique ne peut se contenter d’une simple traduction en un programme mais au contraire va orienter le raisonnement mathématique en tenant compte de problématiques propres à l’informatique.

Atelier 5 : Raisonnements en arithmétique et géométrie discrète – Denise GRENIER Institut Fourier et IREM – Université Grenoble-alpes – CII Université et CII Lycée

L’arithmétique et la géométrie se croisent en géométrie discrète dans des problèmes qui offrent un regard nouveau sur des notions mathématiques classiques et conduisent à des raisonnements spécifiques. Nous étudierons des problèmes originaux accessibles du collège à l’université.

Atelier 6 : Le raisonnement par récurrence : simple à enseigner ? simple à apprendre ? – Denis GARDES et Dominique BERNARD de la CII Lycée.

Après le visionnement de quelques extraits de vidéos à propos du raisonnement par récurrence, nous
présenterons mathématiquement le raisonnement par récurrence. Puis nous analyserons les
productions d’élèves de Terminale lors de tâches liées au raisonnement par récurrence afin
d’identifier les difficultés de compréhension et de mise en œuvre de ce raisonnement. Enfin nous
proposerons des pistes de remédiation.

Atelier 7 :Que les maths seraient simples sans ces fichues variables ! – Zoé MESNIL et René CORI de la CII Lycée.

L’utilisation de variables est une spécificité du langage mathématique, et une source de difficulté majeure pour les élèves. D’autant que ces variables peuvent être soit muettes (liées) soit parlantes (libres), ce qui, ajouté aux nombreuses ambiguïtés de notre langage, n’arrange rien… Par exemple, les quantifications, qui ont pour effet de rendre les variables muettes, sont trop souvent implicites, et cela n’aide pas à la compréhension des propositions, et encore moins à l’appropriation des preuves.
Nous illustrerons ce propos par de nombreux exemples d’expressions mathématiques, d’extraits de manuels.

Atelier 8 : Booléens et preuve de programme – Emmanuel BEFFARA de la C3I

Le type de donnée « booléen » est le plus simple de l’informatique puisqu’il n’a que deux valeurs, généralement appelées « vrai » et « faux ». Cela n’en fait pas l’objet le plus simple à comprendre: il est à la fois lié à la logique (puisqu’il peut représenter les valeurs de vérité classiques), à l’information et son codage (puisqu’il correspond à un bit) et à la programmation (c’est l’ingrédient sur lequel se basent les structures conditionnelles). Le raisonnement sur la correction des programmes met en évidence l’interaction entre ces différents aspects. Le but de cet atelier est d’explorer ce thème, notamment du point de vue de l’enseignement de l’informatique et des mathématiques.

Apport de la logique pour les études didactiques en mathématiques.

Viviane DURAND-GUERRIER Professeure émérite. Université de Montpellier. Institut Montpelliérain Alexander Grothendieck, UMR 5149, CNRS, UM. IREM de l’Académie de Montpellier.

En France, à leur arrivée dans l’enseignement supérieur, les étudiantes et les étudiants sont confrontés à la nécessité d’étudier et d’élaborer par eux-mêmes ou par elles-mêmes des raisonnements et des preuves de plus en plus complexes, ce qu’ils et elles ont peu eu l’occasion de faire dans leurs études secondaires, y compris dans les sections scientifiques. Pour autant, le travail sur le raisonnement est présent au lycée, ainsi que des éléments de logique qui doivent être présentés de manière transversale, c’est-à-dire sans chapitre dédié.

Nous présenterons dans cette conférence les apports de la logique mathématique suivant deux axes. D’une part, comme outil pour les analyses didactiques : nous montrerons en particulier comment la prise en compte des aspects logiques, et notamment des questions de quantification, permet d’enrichir les analyses a priori et a posteriori des situations didactiques proposées aux élèves.  D’autre part, comme objet d’enseignement pour lequel il est nécessaire de trouver une position d’équilibre entre une approche trop formelle dont on sait qu’elle n’est pas efficace, et une approche qui évacuerait les aspects formels dont on sait aussi qu’elle n’est pas efficace en l’illustrant dans le cadre des usages de l’implication à la transition lycée-université.

Cette conférence s’appuiera sur des travaux conduits avec Thomas Barrier et Zoé Mesnil en lien avec deux publications accessibles en ligne :

  Barrier, T., Durand-Guerrier, V., Mesnil, Z. (2019) L’analyse logique comme outil pour les études didactiques en mathématiques. Éducation & Didactique, vol. 13(1), 61-81.  https://journals.openedition.org/educationdidactique/3793?lang=en

Durand-Guerrier, V., Mesnil, Z. (2022). Quelques pistes pour améliorer les usages de l’implication mathématique en début d’université. Épijournal de Didactique et Epistémologie des Mathématiques pour l’Enseignement Supérieur, Vol. 1.
https://doi.org/10.46298/epidemes-7550

Démonstration dans l’histoire. De la logique philosophique à la logique mathématique

Évelyne Barbin, IREM des Pays de la Loire, Laboratoire LMJL de Nantes

Nous proposons d’examiner les liens entre la logique et la démonstration mathématique dans quatre périodes historiques déterminantes. L’Antiquité grecque est celle de la logique d’Aristote et des démonstrations euclidiennes. Au 17^e siècle, mathématiciens et logiciens s’emparent de l’idée de méthode comme art d’inventer, avec le calcul algébrique de Descartes et la logique de Port-Royal, puis le calcul de Leibniz et sa logique graphique. En 1847, les mathématiciens logiciens Boole et de Morgan proposent, l’un une logique algébrique et l’autre une logique formelle. À partir de là, la relation entre mathématiques et logique est beaucoup débattue – inclusion de l’une dans l’autre et laquelle, ou au contraire exclusion –, ainsi que la signification du symbolisme. Dans les années 1879-1881, des logicien(ne)s introduisent des symboles, des diagrammes ou des tables de vérité pour signifier une existence, une relation logique ou l’univers des possibles. Cet historique est destiné à mettre en évidence les différences essentielles entre les approches et les pratiques des philosophes logiciens et des mathématiciens logiciens, afin de penser aux places de la logique, de la démonstration et du symbolisme pour réfléchir sur l’enseignement mathématique.