Cette démarche d’investigation a été proposée à des élèves de 5ème, 4ème, 3ème et de 2nde.
L’objectif est que les élèves mobilisent leurs connaissances arithmétiques en particulier celle sur la division euclidienne.
Dans cette activité, un raisonnement par disjonction de cas est proposé aux élèves.
Les élèves vont être amenés à :
- Choisir et mettre en relation le cadre numérique et des outils algorithmiques pour étudier une situation et résoudre un problème.
- Communiquer, à l’oral en formulant la problématique de travail et à l’écrit en rédigeant sa démarche.
Pré-requis
Afin que les outils mathématiques soient disponibles chez les élèves, un travail autour de la division euclidienne est indispensable. On peut également envisager de travailler sur les raisonnements par disjonction de cas. Un prolongement de cette DI est possible avec l’algorithmique qui devra être préparé en amont, en particulier si les élèves utilisent le logiciel Scratch au collège.
Documents élève
Les élèves résolvent le problème en organisant leur démarche à l’aide de la fiche de narration de recherche.
Un exemple de mise en oeuvre
Modalités de travail
- Travail en groupe de 3 ou 4 élèves
- Classe mobile pour prolongement avec Scratch de l’activité.
- 2 séances :
- Séance 1 : Appropriation, rédaction de la démarche
- Séance 2 : Fin de l’activité, correction et bilan, prolongement Scratch
Déroulé de séances
- Distribution de l’énoncé, lecture individuelle, reprise du vocabulaire.
- Que pensez-vous des raisonnements de la population ?
- 29 = 5 x 5 + 4 = 5 x 4 + 3 x 3 (pourquoi ne pas avoir pris 25 au lieu de 20 ?)
- 38 = 5 x 7 + 3 x 1
- 276 = 3 x 92 + 5 x 0 = 3 x 2 + 5 x 54
Encourager les élèves à donner le multiple de 5 le plus proche en restant inférieur, faire remarquer à tous l’information « maximum de billets ». Enlever des billets pour atteindre un « reste » qui soit un multiple de 3.
- Quelle(s) question(s) mathématiques peut-on se poser ?
Lister les propositions et si la question « Est-ce qu’avec des pièces de 3 et des billets de 5, nous pouvons atteindre tous les nombres entiers supérieurs ou égaux à 8 ? », indiquer que l’on peut conjecturer que cela est vrai grâce à nos premiers essais. - Nous souhaitons que les élèves répondent à la question « Avec des pièces de 3 Soudoks et des billets de 5 Soudoks, comment peut-on obtenir tous les montants entiers supérieurs ou égaux à 8 Soudoks, avec le maximum de billets ? ».
Reformulation : Je veux que pour n’importe quel nombre, vous soyez capables de me donner les calculs, la démarche permettant de calculer le nombre de billets de 5 et de pièces de 3 avec le maximum de billets.
Pour les amener à cela, on peut les interroger sur le côté pratique de la monnaie : « Vous êtes un utilisateur de cette monnaie, vous souhaitez payer quelque chose, qu’est-ce que vous faites ? »
Résolution / Aides
- Les élèves ont des difficultés à mobiliser la division euclidienne par 5 pour avoir le maximum de billets. On peut leur demander : « Combien de billets et de pièces pour payer 72 Soudoks ? »
On peut les ramener à : « Que se passe-t-il entre 29 et 38 ? » et les faire observer les restes de la division euclidienne par 5. - Démarche possible mais difficile pour les élèves à expliquer « comment ».
On cherche le max de billets de 5 : n = q x 5 + … avec q plus grand possible.
Ton reste n’est pas un multiple de 3, qu’est-ce que l’on fait ?
J’enlève un billet, n = (q-1) x 5 + 5 + …
Ton reste est un multiple de 3 ?
Sinon j’enlève un billet, … - Comment les aider à généraliser ? En demandant comment déterminer le nombre de billets.
- Quel est ton premier calcul ? « je cherche combien de fois 5 est le plus proche de mon nombre » : il s’agit de faire une division euclidienne par 5.
- Quels sont les cas possibles quand tu divises par 5 ? Les restes sont entre 0 et 4.
- Comment trouves-tu le nombre maximum de billets grâce à ta DE ? Le quotient.
Démarche attendue
A partir d’exemples, les élèves commencent par effectuer la D.E (division euclidienne) du nombre par 5. On obtient un quotient égal à q et les restes possibles sont : 0, 1, 2, 3 ou 4.
- Si le reste est 0, il y a alors q billets et 0 pièce.
- Si le reste est 3, il y a alors q billets et 1 pièce.
- Si le reste est 2, alors on a : q x 5 + 2 = (q-1) x 5 + 7 = (q-2) x 5 + 12 = (q-2) x 5 + 3 x 4, il y a q-2 billets et 4 pièces.
- Si le reste est 1, alors on a : q x 5 + 1 = (q-1) x 5 + 6 = (q-1) x 5 + 3 x 2, il y a q-1 billets et 2 pièces.
- Si le reste est 4, alors on a : q x 5 + 4 = (q-1) x 5 + 9 = (q-1) x 5 + 3 x 3, il y a q-1 billets et 3 pièces.
Productions d’élèves
Une autre démarche possible
Quand les élèves ont des difficultés à trouver une méthode de résolution, on peut les encourager à travailler sur le chiffre des unités du montant à payer, en leur proposant de réfléchir à 10 nombres consécutifs (on n’évoquera pas directement « le chiffre des unités ») : « Que se passe-t-il entre 10 et 19 ? ». Si les élèves éprouvent des difficultés à trouver le nombre de pièces, on leur propose certains nombres : « Avec 11, combien faut-il de pièces ? ». Quand les élèves obtiennent le résultat correct, on les engage à poursuivre sur d’autres nombres consécutifs. Pour généraliser leur méthode de calcul à tous les autres nombres entiers, les élèves pourront dire qu’à chaque dizaine supérieure, il suffit d’ajouter 2 billets de 5 Soudoks.
De nombreux élèves pourront choisir cette démarche sur le chiffre des unités plutôt que celle sur les restes de la DE par 5. C’est une démarche, étant plus simple à formaliser, est à encourager auprès des élèves afin qu’ils trouvent les solutions du problème. Ensuite, nous pourrons les faire observer que certaines des solutions sont identiques.
Démarche possible sur le chiffre des unités :
- Quand le chiffre des unités est 0 : il faut 0 pièce puis je calcule le nombre de billets en divisant par 5. Le quotient correspond au nombre de billets.
- Quand le chiffre des unités est 1 : il faut 2 pièces puis je calcule le nombre de billets en enlevant 6 au nombre puis je divise par 5. Le quotient correspond au nombre de billets.
- Quand le chiffre des unités est 2 : il faut 4 pièces puis je calcule le nombre de billets en enlevant 12 au nombre puis je divise par 5. Le quotient correspond au nombre de billets.
- Quand le chiffre des unités est 3 : il faut 1 pièce puis je calcule le nombre de billets en enlevant 3 au nombre puis je divise par 5. Le quotient correspond au nombre de billets.
- Quand le chiffre des unités est 4 : il faut 3 pièces puis je calcule le nombre de billets en enlevant 9 au nombre puis je divise par 5. Le quotient correspond au nombre de billets.
- Quand le chiffre des unités est 5 : il faut 0 pièce puis je calcule le nombre de billets en divisant par 5. Le quotient correspond au nombre de billets.
- Quand le chiffre des unités est 6 : il faut 2 pièces puis je calcule le nombre de billets en enlevant 6 au nombre puis je divise par 5. Le quotient correspond au nombre de billets.
- Quand le chiffre des unités est 7 : il faut 4 pièces puis je calcule le nombre de billets en enlevant 12 au nombre puis je divise par 5. Le quotient correspond au nombre de billets.
- Quand le chiffre des unités est 8 : il faut 1 pièce puis je calcule le nombre de billets en enlevant 3 au nombre puis je divise par 5. Le quotient correspond au nombre de billets.
- Quand le chiffre des unités est 9 : il faut 3 pièces puis je calcule le nombre de billets en enlevant 9 au nombre puis je divise par 5. Le quotient correspond au nombre de billets.
La formalisation mathématique de cette méthode est plus compliquée et les pré-requis peuvent être limités à la disjonction de cas. Le raisonnement sur les restes de la DE n’est pas travaillé ici.
Mise en commun, correction, bilan
Bilan maths
- Division euclidienne (avec tous les restes possibles)
Bilan démarche
- raisonnement par disjonction de cas (sur les restes ou sur le chiffre des unités)
- démontrer en explicitant les calculs du nombre de billets (grâce au quotient) et le nombre de pièces (déterminable à l’avance, nombre de cas fini)
Pour mener cette correction et ces bilans en classe, nous pouvons projeter les productions des élèves. Voici un exemple :
Une correction possible pour la deuxième démarche possible

Le bilan mathématique pourra se concentrer sur la recherche de multiples de 5 pour trouver le nombre de billets.
Sujet alternatif
On peut envisager de modifier l’énoncé en proposant des pièces de 3 Soudoks et des billets de 7 Soudoks. Cela permet d’éviter l’écueil du critère de divisibilité par 5 qui ne met pas en relief la résolution avec une division euclidienne par 5.
Prolongement
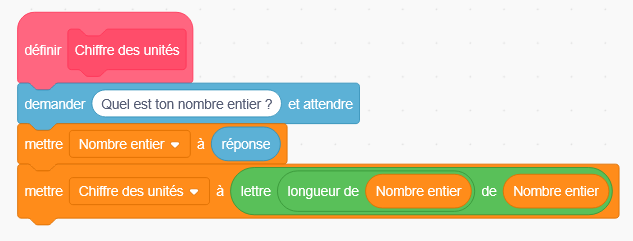
Le prolongement peut également se baser sur la deuxième démarche possible (sur le chiffre des unités). On peut écrire un bloc « chiffre des unités » sur Scratch permettant de récupérer le chiffre des unités d’un nombre afin d’écrire un script complet.