Archives par mot-clé : aire

La situation a été proposée à des élèves de cycle 4 et vise à introduire la distributivité de la multiplication par rapport à l’addition à partir de deux exemples numériques.

Le travail proposé alterne les phases de recherche où les élèves sont en groupes et les mises en commun ou les corrections en plénière.

Les élève sont amenés à :

• calculer l’aire d’un rectangle
• écrire une expression numérique pour résoudre un problème
• communiquer leur démarche

Organisation du travail de groupes

Les élèves seront répartis en un nombre pair de groupes. La moitié des groupes sera nommée « groupes A » et l’autre moitié « groupes B ». On répartira les groupes A en deux sous-groupes : les groupes A1 et A2, de même pour les groupes B en sous-groupes B1 et B2. Il peut y avoir plusieurs groupes A1, A2, B1 et B2 dans la classe.

Documents élèves

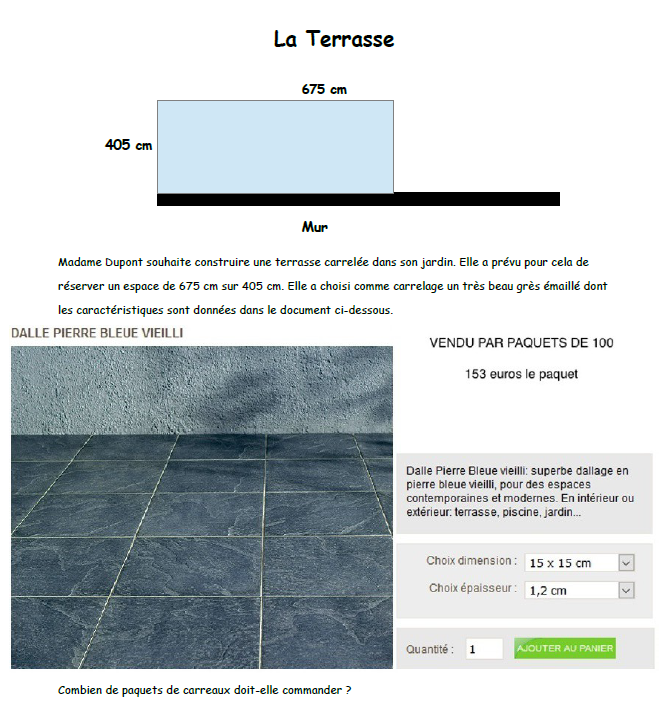
Un exemple de mise en œuvre

Modalités de travail

• Travail de groupes de 4 élèves (nommés A1, A2, B1 ou B2)
• Prévoir 3 séances : 2 x 30 min pour la première partie, 1h pour la deuxième partie.

Déroulement

Étape 1

Nous distribuons l’énoncé de la première partie aux groupes en indiquant qu’ils ont le même problème mais avec des valeurs numériques différentes.

Cette première étape est destinée à s’assurer que les élèves ont le bon nombre de carreaux restant et qu’ils disposent tous de la formule de calcul de l’aire du rectangle. Nous veillons à ne pas parler de calcul de superficie de la terrasse pour ne pas orienter les procédures des élèves.

Nous demandons aux élèves de rédiger leur démarche et leur réponse à la question posée sur une feuille que nous ramassons à la fin de la recherche.

Étape 2

Lors de la séance suivante, nous proposons aux élèves une correction en utilisant une fausse copie qui reprend des éléments de leurs productions. En plénière, nous y apportons des compléments et des modifications pour qu’elle constitue une solution bien rédigée du problème.

A la fin de cette séance, nous engageons la discussion avec les élèves autour des carreaux restants. Lors de ces échanges, l’idée d’agrandir la terrasse est évoquée et nous indiquons que ce sera l’objectif du travail de la prochaine séance.

Étape 3

Lors de la troisième et dernière séance, les groupes se reforment et nous distribuons l’énoncé de la deuxième partie à chaque sous-groupe. Les questions intermédiaires différentes amènent les élèves à procéder de deux façons différentes pour calculer la surface de la nouvelle terrasse : les groupes A1 et B1 obtiennent une expression numérique sous forme développée, tandis que les groupes A2 et B2 obtiennent sa forme factorisée. La mise en commun a pour objectif de mettre en évidence l’égalité des deux écritures. Nous projetons un fichier Geogebra qui permet de visualiser les démarches des groupes.

Nous complétons en plénière le bilan proposé pour les deux énoncés en veillant à écrire les égalités correctement pour mettre en évidence le développement et la factorisation des expressions numériques. La généralisation avec des lettres peut être difficile, avec des élèves de début de cycle 4, nous nous contentons de proposer d’autres exemples numériques pour retravailler ces notions. Pour des élèves de milieu de cycle 4, la généralisation peut être menée en classe avec l’aide du professeur.

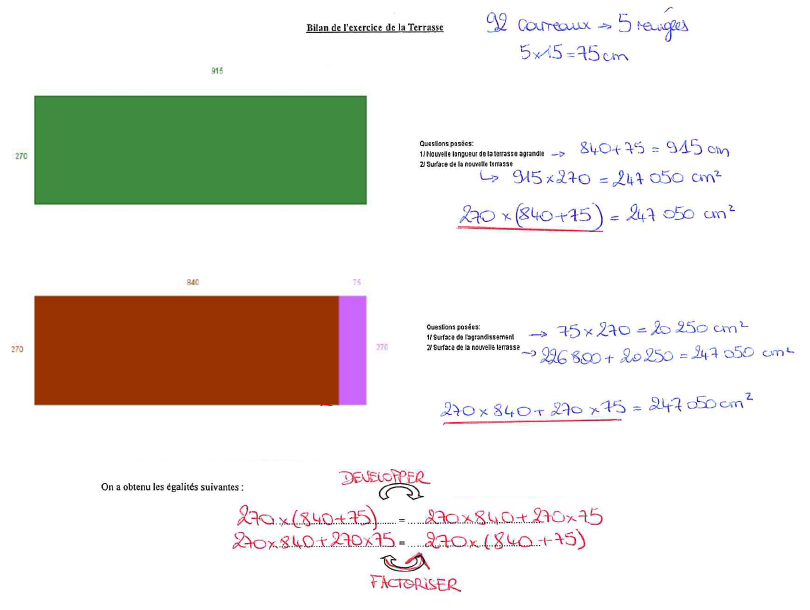
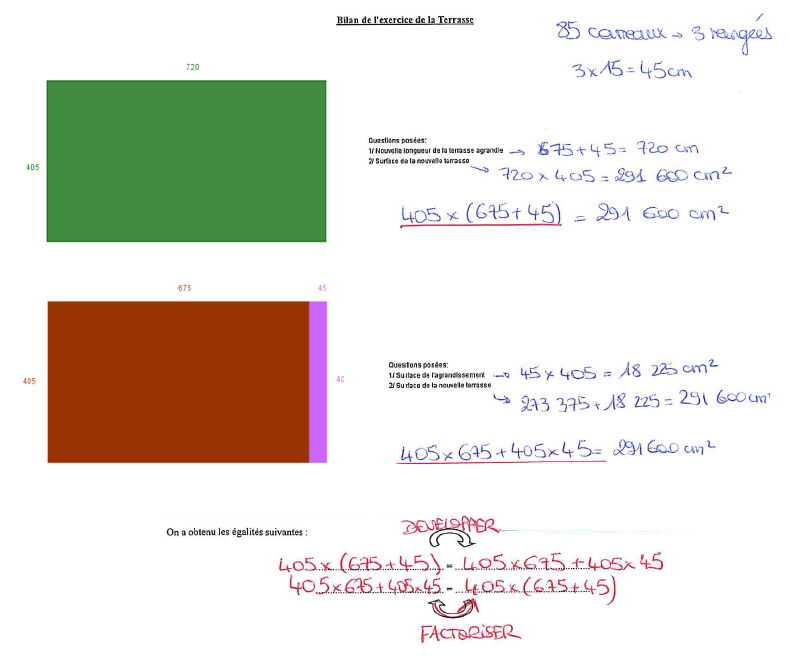
Productions d’élèves

Voici quelques productions de groupes lors du travail de la première partie.

Voici le fichier avec l’énoncé pour les élèves