Archives par mot-clé : tice

Le jardin

Présentation

Nous proposons l’exercice du jardin destiné aux élèves de 3ème  permettant de réinvestir la notion de fonction, et notamment de travailler sur la compétence « modéliser » (valider ou invalider un modèle).

Les élèves vont être amenés à :

  • Tester des valeurs.
  • Réinvestir les connaissances sur les aires.
  • Émettre une conjecture.
  • Modéliser la situation à l’aide du logiciel Geogebra

Pré-requis

Aire des figures usuelles, utilisation d’un repère, utilisation du logiciel Géogébra.

Documents élèves

Un exemple de mise en œuvre

  • Modalités
    • Travail individuel ou en binôme
    • Une séance d’une heure
    • Une classe mobile (à privilégier) ou en salle multimédia

  • Déroulement

Question 1:
Les élèves répondent à la première question afin de s’approprier le problème. Ils font des essais avec différentes positions du point P et donc différentes valeurs pour la longueur AP.

Au tableau, on récolte les valeurs calculées par les élèves.

Question 2 :
Une mise en commun permet de relever les valeurs trouvées (très rapidement les élèves voient la nécessité de les organiser dans un tableau) et certains proposent de les représenter à l’aide d’un graphique.
Les élèves conjecturent l’aire minimale ainsi que la distance AP associée à l’aide du graphique et du tableau.

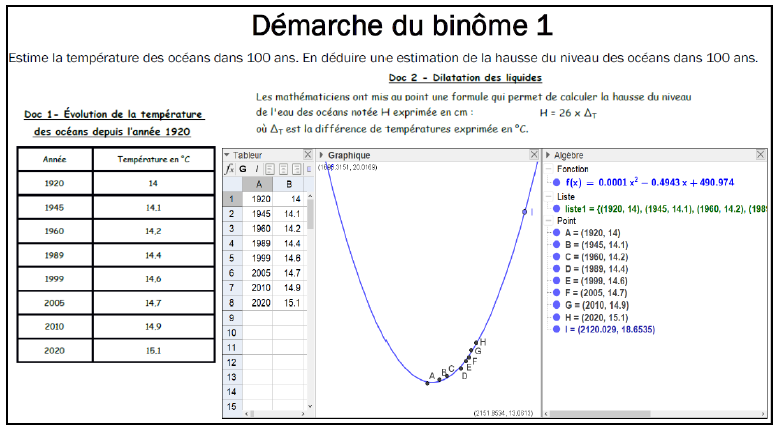
En bilan de cette activité, nous utilisons le logiciel Geogebra pour présenter aux élèves une démarche qu’ils pourront réutiliser dans d’autres situations (par exemple, pour l’exercice de la plage) grâce au document suivant qui est distribué. Les élèves reproduisent la manipulation proposée, qui n’est pas exigible pour un élève de collège.

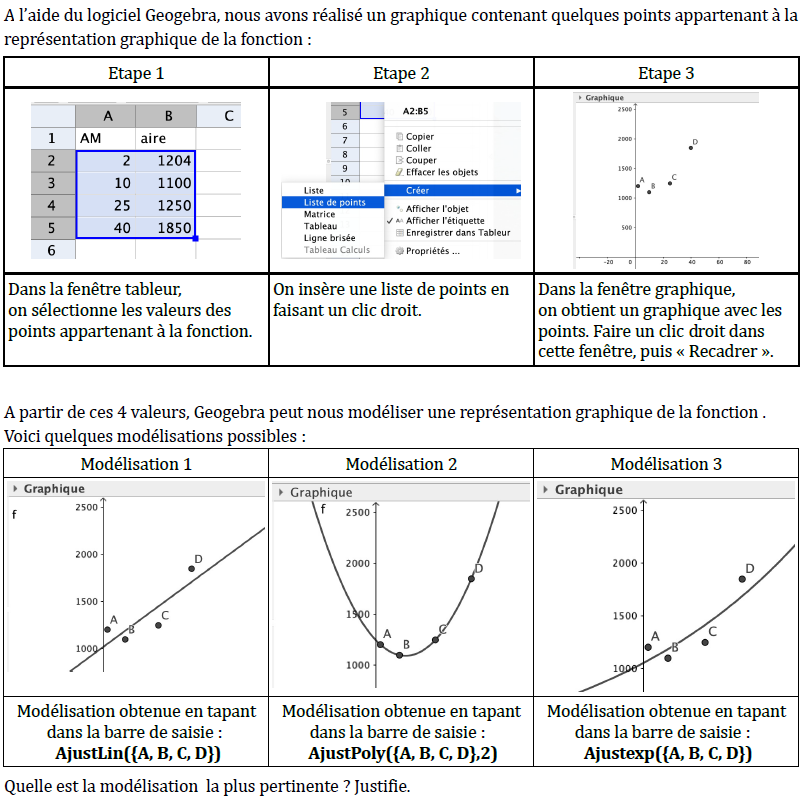
La présentation des outils numériques est réalisée par le professeur afin de montrer leur intérêt :

« la réalisation du nuage de points est plus rapide avec Geogebra et le tracé de la courbe est plus précis qu’à la main ».

Les élèves s’accordent pour dire que la courbe qui passe par le plus de points possibles est la modélisation la plus pertinente et choisissent donc la modélisation 2 pour représenter l’aire du jardin en fonction de la distance AP. Puis en plaçant un « point sur objet » et en le déplaçant, les élèves conjecturent le minimum de l’aire du jardin et en déduisent la position du point P sur le segment [AB].


Cette démarche a permis aux élèves de valider leur conjecture, en ayant une approche scientifique du problème. En utilisant la modélisation de la situation grâce au logiciel Géogébra, ils ont pu répondre à la question sans utiliser une expression algébrique qui aurait mené à une impasse. (Minimum d’une fonction du second degré )

  • Trace écrite des élèves

Voici un exemple de trace écrite pour cette activité.

L’aire du jardin dépend de la position du point P.
On peut exprimer et représenter l’aire du jardin en fonction de la longueur AP ( Graphique, tableau, …).
Pour résoudre ce type de problème, Geogebra peut nous proposer des modélisations possibles à partir de quelques points dans le graphique.
Selon la situation, il faut choisir la modélisation la plus adaptée.

La plage

Afin d’aider les élèves de 3ème à appréhender le monde qui les entoure, nous avons décidé d’aborder le thème du réchauffement climatique. Le but est de faire le lien entre la hausse de la température des océans et la montée du niveau de l’eau.

Les élèves vont être amenés à:

  • modéliser la température des océans en fonction des années.
  • réinvestir les connaissances de géométrie plane.
  • répondre à une problématique.

Cette démarche d’investigation admet une mise en œuvre collaborative, les élèves mettent en évidence deux étapes de résolution et se répartissent les tâches avant de mettre en commun leurs résultats pour résoudre le problème.

Pré-requis

Notion de fonction, théorèmes de géométrie (Pythagore et Thalès ou triangles semblables), utilisation de Geogebra.

Documents élèves

Afin de donner du sens à notre problème, nous avons fourni l’article scientifique et les documents de recherche suivants :


Un exemple de mise en oeuvre

Modalités

  • Travail de groupe: 4 élèves qui se répartissent en 2 binômes
  • Deux séances d’une heure
  • Une classe mobile


Déroulement

Etape1

Lecture de l’article scientifique et débat en classe pour s’assurer de l’engagement dans le problème.

Etape 2

Lecture et utilisation des documents de recherche pour répondre aux premières questions :

Ces questions permettent de s’assurer de la compréhension et d’accompagner l’utilisation des documents pour tous les élèves.

Etape 3

Les deux étapes précédentes sont essentielles afin que les élèves s’investissent dans la résolution du problème qui va suivre.
Une discussion permet d’amener la question : « Dans combien d’années la plage sera recouverte par l’eau ? « .

On aboutit à deux sous-problèmes :

Deux binômes se forment dans chaque groupe.
On attribue à chaque binôme la résolution d’un des problèmes.

Les élèves du binôme 1 doivent estimer la température en 2120 (ordonnée du point I). Nous avons fait le choix d’utiliser le logiciel Geogebra afin de mettre en avant l’outil informatique.
NB : Nous avions travaillé cette démarche lors de l’introduction de la notion de fonction avec l’exercice du jardin.

Les élèves du binôme 2 doivent mobiliser les théorèmes de Pythagore et de Thalès afin de déterminer la hauteur de la plage. dans un deuxième temps, ils déterminent la température associée à cette hauteur.

Etape 4

Les deux binômes mettent en commun leur travail pour répondre à la problématique:  » Dans combien d’années la plage sera recouverte par l’eau ? « .

A partir de la température déterminée par le binôme 2, les élèves utilisent le fichier Geogebra du binôme 1 (en déplaçant le point I) pour estimer l’année correspondante.

Etape 5

Nous réalisons un bilan avec tous les groupes:

  • les mathématiques peuvent être un outil de prévision.
  • le réchauffement climatique a un impact fort sur notre environnement.


Productions d’élèves